Dijkstra Maps Visualized
Dijkstra Maps Visualized
Dijkstra maps are awesome. They can teach your AI some clever new tricks - and cheaply, too, because the same map can be used for any number of actors. And AI is just the beginning: Dijkstra maps can facilitate automatic exploration, pathfind-to-cursor, and dungeon generation, too.
So, what is a Dijkstra map? Take a look:
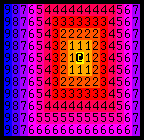
At its most basic, it indicates distances. In the above image, the map shows how far from the player ('@') each cell is. (The colors here are just for demonstrative purposes. The numbers are the important part.)
Now, I'd like to encourage you to read this fantastic article by Pender(Brian Walker), the creator of Brogue. This article is based heavily on the ideas presented there, and I'll go into more detail on how they can be achieved.
Finished reading that one? Sounds amazing, right? Let's see if we can get those examples working.
-- The basics --
One of the simplest applications of Dijkstra maps is making enemies beeline for the player, taking the shortest path at all times. The image above is all you need. These goblins -
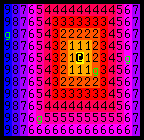
- can, each turn, simply check each cell adjacent to them, and step to any that has the lowest value.
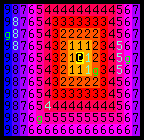
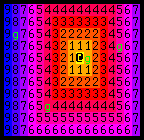
This map only needs to be updated when the player moves, like this:
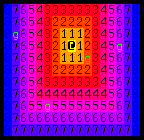
-- Multiple sources --
They work great! If you have multiple sources, the resulting map will lead toward whichever is closest. In this example, we add gold. Goblins now want to attack the player AND collect gold:
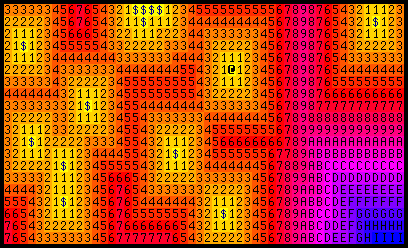
(The map will be updated whenever the player moves or gold is collected, so the goblins don't aim for a target that's no longer there.)
-- Variable strengths, and what distance really means --
So, in the previous example, our goblins were happy to collect gold or attack the player, whichever was closest, just by seeking lower values on the map. But what if we want our goblins to be exceptionally greedy, willing to walk farther to reach gold even if the player is actually closer? Here's how.
Instead of starting all of our sources at a value of 0, give the more desirable ones a lower value - let's use -4 for the gold while keeping the player at 0. Like this:
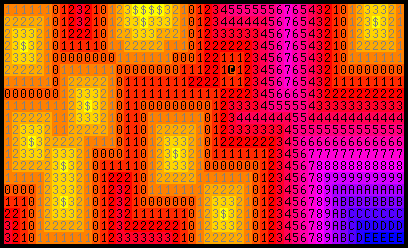 (Those gray numbers are negatives, so a goblin seeking lower values would move from a 0 to a -1 and so forth.)
(Those gray numbers are negatives, so a goblin seeking lower values would move from a 0 to a -1 and so forth.)
Why does this work? By starting the gold at a value of -4, we're treating it as though it were closer than it really is. If a goblin is 7 cells away from gold, and 3 cells away from the player, the -4 modifier means that the goblin will see them as equidistant, and be equally likely to approach either one.
-- Fleeing AI --
Now that we know how to make enemies approach, let's look at making them flee. What happens if we take the approach map and have them move toward higher numbers? (i.e., darker colors?)
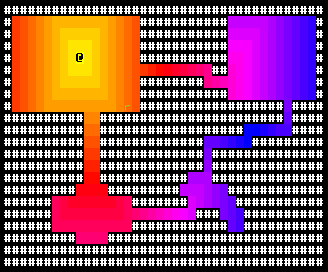
They just end up in the corners, and can't escape even when the player is right next to them. Here's how to fix that:
First, take the existing approach map and multiply each value by a number close to -1.2. This effectively flips the map so that moving toward the lower numbers (lighter colors) takes you away from the source(s) instead of toward the source(s).
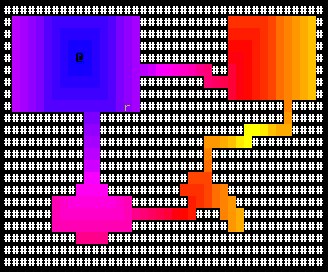
Then, we rescan that map. It's the same as the basic scan, but we use whatever values happen to be in the map already. After that, we end up with this:
Observe what happened to the spaces around corners and doorways.
Note also that what we've effectively done is to create a new map using the farthest tiles as the sources, and giving them a bonus for being farther away - the bonus is the 0.2 part of the -1.2 multiplication.
Changing that coefficient from -1.2 to a stronger number can have a big effect on the result: The bigger the coefficient, the "closer" a distant cell will be, and the more it'll "pull" fleeing monsters toward it. Here's what a coefficient of -1.6 looks like:
If the coefficient is too high, the most distant cells will dominate the whole map - a fleeing monster will ONLY want to move to the FARTHEST cell if this happens. If the coefficient is too low, the map won't change very much from the "bump into corners" version. Experiment with different values to see which you like!
-- Automatic exploration --
Autoexplore is really easy! Just use every unseen cell as a source, and you get this:
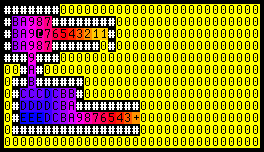
The player can now move toward lower values and automatically uncover new territory. Keep doing this each turn until a key is pressed or until something happens (an enemy comes into view; a message is generated; the player takes damage).
(Note that this even accounts for the extra turn required to open a door ('+') before you move through it, by assigning it a cost of 2 instead of 1.)
-- Cheap mouse pathing --
Let's say you want to show a visible path onscreen as the player moves the mouse (or other) cursor across the map. Dijkstra maps can provide an optimization so you don't need to run a normal pathfinder (like A* or regular Dijkstra pathfinding) every time the cursor moves to a new cell.

By calculating a single Dijkstra map when the cursor moves onto the map (for the first time on each turn), you can simply roll from the cursor to the player to find a path (then, of course, reverse that path so it leads from the player to the cursor).
(I recommend having a way to ensure that the path you see is the path you take - I prefer a deterministic pathfinding routine for the player, and a randomized one for enemies.)
Like autoexplore, this one treats unexplored cells like they're regular floors, so it's possible to choose an impossible path. That's fine - you'll just need to stop the player once it's clear that the chosen path leads into a wall.

-- Moving into optimal range --
Want your ranged enemies to stay at a certain range? Start with a Dijkstra map from the player, and then create another one - the source cells will be the cells on the first map with the desired range:

But, you probably want to go one step further, and say that the source cells will be the cells on the first map with the desired range...to which the player has line of sight:

-- Hazard avoidance --
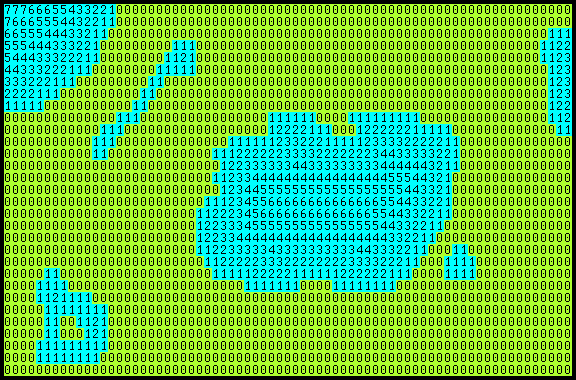
If the player can swim, but only for a few turns, you can use a map like this one, calculated just once when the map is created. Track the remaining swimming turns, and if the player tries to move to a cell with a value greater than the remaining turns, you can prevent that move and give a warning.
I hope these examples help to illustrate just how useful Dijkstra maps can be. Good luck!