Hexagonal Tiles
Most roguelikes use a grid of square cells to represent the game world. An alternative is to use a grid of six-sided hexagons. Many pen & paper wargames use hexes, but they are much less common on computers, since working with them involves some technical trickiness.
The nice thing with hexes is that movement in any of the six directions can be treated in the exact same way in game logic. With square tiles, diagonal movement has a different movement length and can be blocked by obstacles in two cells adjacent to the diagonal connection.
Coordinate systems with a hex grid
There are several possible coordinate systems.
- Skewed axis. An easy way of staying sane while working with a hex grid is to just treat it internally as a square grid where travel along one diagonal is permitted, and travel along the other is not.
-----
/ \
/ _o_ \
\_- -_/
-\ /-_
| ----- x-axis
y-axis
So assuming that's hex at x=0, y=0, or (0, 0), the one on the lower right would be (1, 0), the one on the lower left (0, 1) and the one right below is (1, 1). Now you can write your game logic as just using regular x, y coordinates, and allow movement in cardinal directions and along the (1, 1) diagonal. Angles between vectors in these coordinates won't be right though, but this is good enough for simple logic.
This is a special case of oblique coordinates (with a 60° angle).
- Even-only. Have usual (x,y) coordinates, but only pairs whose sum is even denote hex grids. Thus, the neighbors of (0,0) are (2,0), (-2,0), (1,1), (1,-1), (-1,-1) and (-1,1). This is the most natural coordinate system when using an ASCII representation like this:
. 4 . . . . .
. . . . . .
. 2 . . . . .
. . . . . .
. 0 2 4 6 8 .
The advantage of this system is that rectangular arrays will really be rectangular (while the system above naturally leads to level in a shape of a paralellogram). This feature makes it easier to create rectangular rooms etc. A disadvantage is that you get lots of "dead space" in your arrays (but it is possible to overcome this by using arr[y][x>>1] for indexing arrays, or by using arr[y][x] for partial information about a hex grid and arr[y][x^1] for the other part).
- Zigzagged axis. Have an axis which is not straight, like here:
0 1 2 3 A 0 0 0 0 B
0 1 2 3 1 1 1 1 (A) X coordinates
0 1 2 3 2 2 2 2 (B) Y coordinates
0 1 2 3 3 3 3 3
This method also has the advantage that rectangular arrays are rectangular, without the disadvantageous "dead space". A big disadvantage here is that it is no longer possible to add vectors by simply adding both of their coordinates.
- Symmetrical XYZ axis. Imagine the set of points with integer coordinates such that x+y+z=0. They are all on the same plane, and after you rotate it, you get a coordinate system on a plane with hexagonal tiles. Some formulae are nice in this system.
- One more coordinate system: [1]
Note that by using the even-only method with arr[y][x>>1] array indexing you combine advantages of even-odd and zigzagged axis, without any of their disadvantages.
Fake isometric walls
A fun property of hexes is that they look kind of like isometric cubes. Lines that are coincidentally along the x and y axes we picked above, as seen in the screenshot for the Downfall roguelike, look a lot like walls in an isometric game. Of course this is a trick, since you can move in three directions from the obtuse vertical corners and in only two directions from the acute horizontal corners, while in a real isometric game all the corners would be symmetric.
You can do something similar with ASCII graphics by alternating between hex-equivalent cells and empty space, and using cabinet projection:
. o - - - - > x-axis
. / . # # # # .
/ . # . . # .
v . # . . . .
|. # # # # . .
y-axis
In which case map tile <X, Y> is drawn at <2*X + mapHeight - Y, Y> (in the skewed axis coordinate system, in the even-only system this is simply (X, Y) and in the zigzagged axis system it is (2X+Y mod 2, Y)).
Slightly less fake graphical isometric walls
If you want to go the graphical route, using these formulas for the hex/isometric to cartesian transformation while replacing sin(angle) with 1/2 and cos(angle) with 1 would give a pretty good approximation of angle= 26.57 degrees and is a useful simplification:
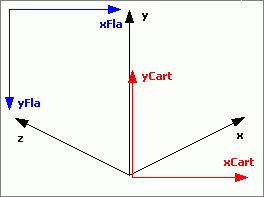
function xFla(x, y, z) {
var xCart = (x-z);
return xCart+xOrigin;
};
function yFla(x, y, z) {
var yCart = y+(x+z)/2;
return -yCart+yOrigin;
};
Or, assuming a 2d game (y=0):
function xFla(x, z) {
var xCart = (x-z);
return xCart+xOrigin;
};
function yFla(x, z) {
var yCart = (x+z)/2;
return -yCart+yOrigin;
};
Distance on a hex grid
Using the skewed axis coordinate system above, you can get the hex grid length of a vector with the following function:
def dist(x, y):
if x * y < 0: # x and y have opposite signs
return max(abs(x), abs(y))
else:
return abs(x) + abs(y)
You can get the distance between points (x1, y1) and (x2, y2) with dist(x2-x1, y2-y1).
See also
- See the Geometry article for a comparison with other geometries used in roguelikes, with lists of roguelikes using each system.
References
- Amit Patel's hex tile programming articles: http://www-cs-students.stanford.edu/~amitp/gameprog.html#hex